Transient climate response (TCR) is defined as the change in global temperature after a doubling of CO2 during a simulation where atmospheric CO2 increases at 1%/year. But, is TCR a constant?
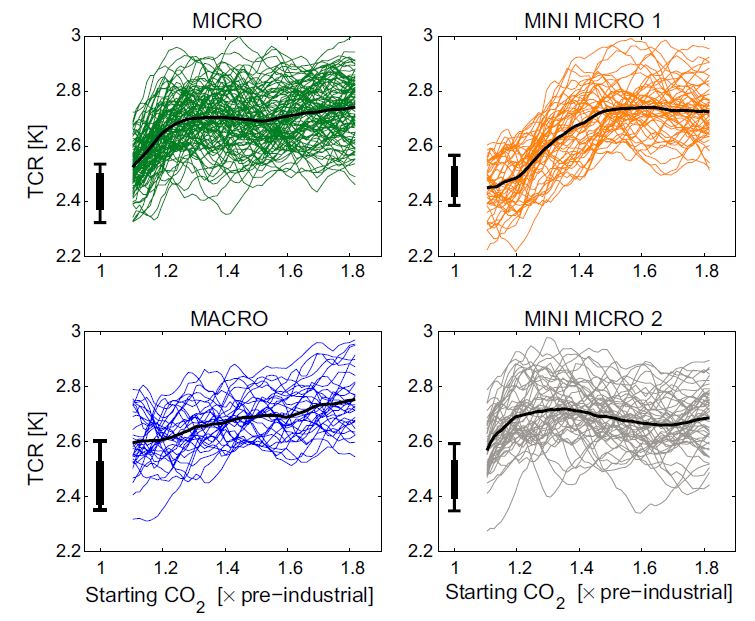
The previous post described a set of simulations with the FAMOUS climate model in which we ran 230 different realisations of increasing CO2 at 1%/year for 140 years. [The difference between the types of ensemble (MICRO & MACRO) are not important for this post.]
The figure below shows TCR estimated in the usual way, over the first 70 years of the simulation (black bars). Note that there is a range of TCR from the different realisations of future climate. This uncertainty is around 0.1K, demonstrating that estimating TCR from a single member (as is normally done) is reasonable – this is a much smaller uncertainty than the range between models for example.
It is also possible to estimate TCR over all later 70-year periods in which CO2 also doubles. It is clear that, in this model, TCR increases as the climate warms – i.e. TCR estimated from years 71-140 is larger than from years 1-70. Although this might be due to committed warming adding to the later estimates, it is also possible that TCR may not be constant.
The climate sensitivity during interglacials is clearly well below 1. We are currently in an interglacial, so the climate sensitivity will still be below 1.
What you are instead talking about is the theoretical climate sensitivity, which is overwhelmingly caused by academic obsession with the late 20th century NATURAL warming. (plus perhaps a very small amount of women-made warming).
And that theoretical figure will come down and down and down toward the real level as the effect of the short term warming which so obsesses academia fades into the data.
DS = 4sigma.epsilon.T^3 DT
For DS = 5.3ln(2). Then DT = TCR
Therefore TCR is temperature dependent and goes like T^-3
TCR(290) = TCR(288) . 288^3/290^3 = 0.98TCR(288)
So climate sensitivity should get smaller the more it warms !
Sorry a bit terse. I am typing on my phone while bouncing around on a ferry!
Firstly, I don’t think your calculation above is for the TCR; it would be more for the ECS. Also, the Planck response is not the only feedback factor that is/could be non-linear. I can’t find it at the moment, but I did recently read a paper that was also trying to estimate the non-linearities in the water vapour feeback. What you say above would only be correct if we assumed that all we have to consider is the radiative response to a doubling of CO2 and the Planck response.
Also, I think that some of the non-linearity can come from things like polar amplification (for example) rather than from true non-linearities in the feedbacks. If different regions warm at different rates, then the global response might appear non-linear, even if the actual non-linearities in the feedbacks isn’t significant.
Hi Ed your paper raises a multitude of “avenues” on TCR. On a cursory reading it seems rather ground breaking. I think that TCR could be variable depending on the initial conditions of any given period of a doubling of CO2. Those initial conditions are not easy to determine though the state of the oceans are prime candidate IMO.
It, a variable TCR, raises the interesting possibility of not only explaining the “hiatus” but also a possible fall in GMST after this period despite rising emissions(obviously this is not a slam dunk).
If the initial conditions are mostly internally derived, in a sense reflecting all that has gone before in the climate system, which to me seems intuitive then what happens next will be modulated by the past, whatever we do has “irreducible uncertainty”attached?
Which leads to your question “are pauses followed by surges?”
Am I on the right track here?
Does TCR depends on how a model is spun up?
How much can the initial (spun-up) state of a climate model vary, from one run to another?
Liang et al looked at similar issues: http://journals.ametsoc.org/doi/abs/10.1175/JAS-D-12-0338.1
I think there are probably small effects from this, but not enough to explain CMIP5 model range.
cheers,
Ed.